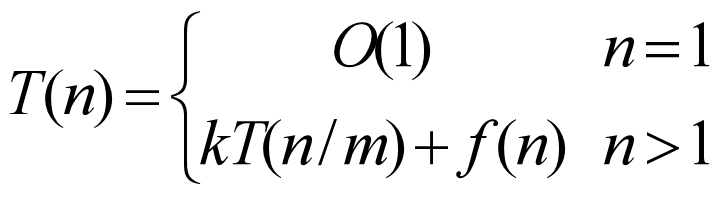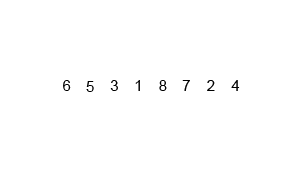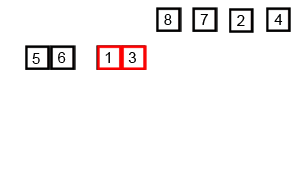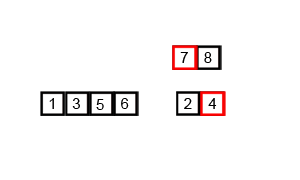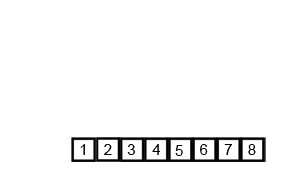复习内容

算法概述—复杂度分析（时间、空间）
分治法
动态规划
贪心算法
回溯法
分支限界法

分治法

基本思想：将一个规模为n的问题分解为k个规模较小的子问题，些子问题互相独立且与原问题相同。递归地解这些子问题，然后将各个子问题的解合并得到原问题的解。

分治法在每一层递归上都有三个步骤：

分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；
解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题；
合并：将各个子问题的解合并为原问题的解。

分治法所能解决的问题一般具有的几个特征是：
（1）该问题的规模缩小到一定的程度就可以容易地解决；

（2）该问题可以分解为若干个规模较小的相同问题;

（3）利用该问题分解出的子问题的解可以合并为该问题的解；

（4）原问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

分治法的时间复杂性分析

经典例题：二分搜索、归并排序、棋盘覆盖、选择问题等

归并排序

第14周13–第8章排序13–8.5归并排序_哔哩哔哩_bilibili

归并排序需要的空间就和原来的数组大小一样

【算法】排序算法之归并排序 - 知乎 (zhihu.com)

https://www.bilibili.com/video/BV1Pt4y197VZ/?spm_id_from=333.788.recommend_more_video.0&vd_source=2259e5459a8cfd21bcf92bc46bf3beda

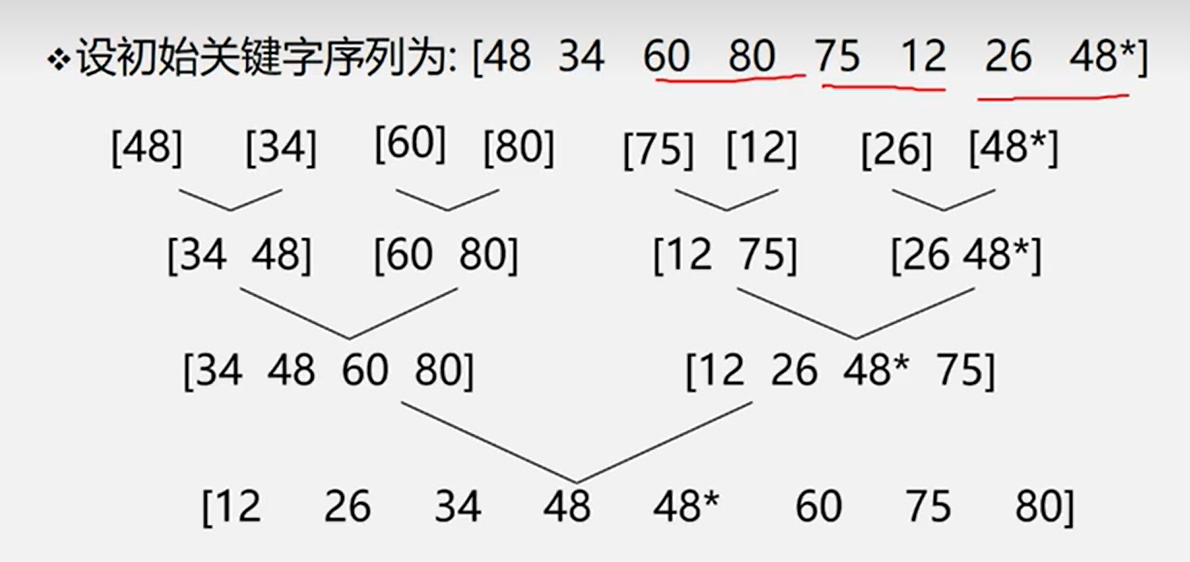
归并排序，是创建在归并操作上的一种有效的排序算法。算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。归并排序思路简单，速度仅次于快速排序，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列。

1. 基本思想

归并排序是用分治思想，分治模式在每一层递归上有三个步骤：

分解（Divide）：将n个元素分成个含n/2个元素的子序列。
解决（Conquer）：用合并排序法对两个子序列递归的排序。
合并（Combine）：合并两个已排序的子序列已得到排序结果。

2. 实现逻辑

2.1 迭代法

① 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
② 设定两个指针，最初位置分别为两个已经排序序列的起始位置
③ 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
④ 重复步骤③直到某一指针到达序列尾
⑤ 将另一序列剩下的所有元素直接复制到合并序列尾

2.2 递归法

① 将序列每相邻两个数字进行归并操作，形成floor(n/2)个序列，排序后每个序列包含两个元素
② 将上述序列再次归并，形成floor(n/4)个序列，每个序列包含四个元素
③ 重复步骤②，直到所有元素排序完毕

3. 动图演示

归并排序演示

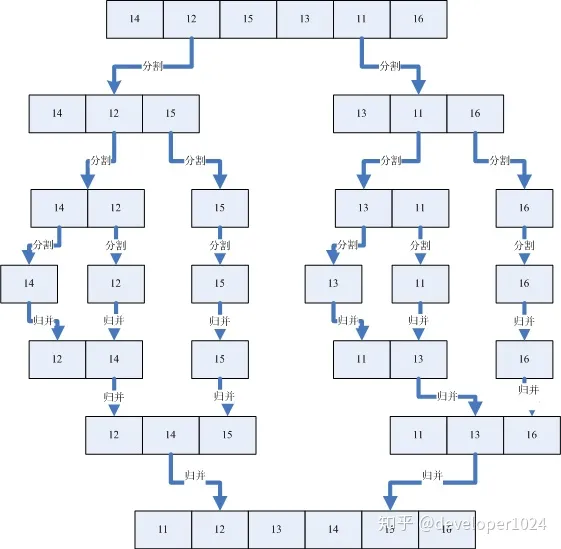
具体的我们以一组无序数列｛14，12，15，13，11，16｝为例分解说明，如下图所示：

上图中首先把一个未排序的序列从中间分割成2部分，再把2部分分成4部分，依次分割下去，直到分割成一个一个的数据，再把这些数据两两归并到一起，使之有序，不停的归并，最后成为一个排好序的序列。

4. 复杂度分析

平均时间复杂度：O(nlogn)
最佳时间复杂度：O(n)
最差时间复杂度：O(nlogn)
空间复杂度：O(n)
排序方式：In-place
稳定性：稳定

不管元素在什么情况下都要做这些步骤，所以花销的时间是不变的，所以该算法的最优时间复杂度和最差时间复杂度及平均时间复杂度都是一样的为：O( nlogn )

归并的空间复杂度就是那个临时的数组和递归时压入栈的数据占用的空间：n + logn；所以空间复杂度为: O(n)。

归并排序算法中，归并最后到底都是相邻元素之间的比较交换，并不会发生相同元素的相对位置发生变化，故是稳定性算法。

5. 代码实现

5.1 C版本

迭代法：

// 归并排序（C-迭代版）
int min(int x, int 
        y) {
    return x < y ? x : y;
}
void merge_sort(int arr[], int len) {
    int* a = arr;
    int* b = (int*) malloc(len * sizeof(int));
    int seg, start;
    for (seg = 1; seg < len; seg += seg) {
        for (start = 0; start < len; start += seg + seg) {
            int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        int* temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        int i;
        for (i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    free(b);
}

递归法：

// 归并排序（C-递归版）
void merge_sort_recursive(int arr[], int reg[], int start, int end) {//0，9
    if (start >= end)
        return;
    int len = end - start;//9 
    int mid = (len /2) + start;//4
    int start1 = start;//0
    int end1 = mid;//4
    
    int start2 = mid + 1;//5
    int end2 = end;//9
    merge_sort_recursive(arr, reg, start1, end1);//排序左半部分
    merge_sort_recursive(arr, reg, start2, end2);//排序右半部分
    int k = start;//0 这个的意思是reg数组的下标
    while (start1 <= end1 && start2 <= end2)
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];//合并左半部分和右半部分
    while (start1 <= end1)//如果左面都比较大，右面的都进去了，那就把左边的全加到后面
        reg[k++] = arr[start1++];
    while (start2 <= end2)////如果右面都比较大，左面的都进去了，那就把右边的全加到后面
        reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
        arr[k] = reg[k];
}
void merge_sort(int arr[], const int len) {//需要排序的数组，数组长度//10
    int reg[len];//定义保留空间
    merge_sort_recursive(arr, reg, 0, len - 1);//意思是需要从0到9进行排序//9
}

动态规划

基本思想：将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。求解过程中，为避免对相同的子问题重复求解，用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中

算法设计步骤：

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

基本要素：(1) 最优子结构性质（2）子问题重叠性质

经典例题：矩阵连乘积问题、0-1背包问题、最长公共子序列问题、最大子段和问题等

0-1背包问题

时间复杂度O（nW）

带你学透0-1背包问题！| 关于背包问题，你不清楚的地方，这里都讲了！| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili

https://programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html#%E4%BA%8C%E7%BB%B4dp%E6%95%B0%E7%BB%8401%E8%83%8C%E5%8C%85

背包最大重量为4。

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

void test_2_wei_bag_problem1() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagweight = 4;

    // 二维数组
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));

    // 初始化
    for (int j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    // weight数组的大小 就是物品个数
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

        }
    }

    cout << dp[weight.size() - 1][bagweight] << endl;
}

int main() {
    test_2_wei_bag_problem1();
}

贪心算法

基本思想：在求最优解问题的过程中，依据某种贪心标准，从问题的初始状态出发，直接去求每一步的最优解，通过若干次的贪心选择，最终得出整个问题的最优解。

贪心算法的基本要素：贪心选择性质；最优子结构性质

经典问题：背包问题、最优装载问题、单源最短路径问题、最小生成树问题等

最小生成树问题：

让你两分钟学会最小生成树_哔哩哔哩_bilibili

最优装载问题

最优装载问题的时间复杂度主要在sort


package 算法考试;

import java.util.Arrays;

/**
 * 最优装载问题（贪心算法） 
 * @author ruochen
 * @version 1.0
 */
public class LoadingProblem {
	private static int[] x; 

	/**
	 * 
	 * @param c 总重量
	 * @param w 每个集装箱的重量
	 * @param x 记录是否装入 （1： 装入    0： 不装入）
	 * @return
	 */
	public static float Loading(float c, float[] w, int[] x) {
		int n = w.length;
		Element[] d = new Element[n];
		for (int i = 0; i < n; i++) {
			// 初始化
			d[i] = new Element(w[i], i);
		}
		Arrays.sort(d);
		// 记录最优值
		float opt = 0;
		for (int i = 0; i < n; i++) {
			// 初始化 
			x[i] = 0;
		}
		for (int i = 0; i < n && d[i].w <= c; i++) {
			x[d[i].i] = 1;
			opt += d[i].w;
			c -= d[i].w;
		}
		return opt;
	}
	
	public static void main(String[] args) {
		float c = 10;
		float[] w = new float[]{4, 2, 5, 1, 3};
//		float[] w = new float[]{1,10};
		x = new int[w.length];
		float opt = Loading(c, w, x);
		System.out.println("最优值为: " + opt);
		System.out.println("最优解为： " + Arrays.toString(x));
	}
	
	public static class Element implements Comparable<Element> {
		float w;
		int i;
		
		public Element(float w, int i) {
			this.w = w;
			this.i = i;
		}
		
		/**
		 * 按照升序排列
		 */
		@Override
		public int compareTo(Element o) {
			if (this.w < o.w) 
				return -1;
			else if (this.w == o.w)
				return 0;
			else 
				return 1;
		}
	}
}

回溯法（这个到时候看课本上的代码！！）

基本思想：回溯法的基本做法是搜索，在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对该结点为根的子树的搜索，逐层向其祖先结点回溯；否则，进入该子树，继续按深度优先策略搜索。

经典例题：皇后问题、装载问题、图的m着色问题、 0-1背包问题、子集和问题

子集和问题

回溯算法解决子集问题，树上节点都是目标集和！ | LeetCode：78.子集_哔哩哔哩_bilibili

代码随想录 (programmercarl.com)

43分钟开始子集和问题：

时间复杂度 O（2^n）,解空间树中有 2^ (n+1) -1个结点

回溯法状态空间树、剪枝函数蒙特卡罗解的估计 n-皇后程序子集和数的状态空间树_哔哩哔哩_bilibili

package 算法考试;

import 算法考试.Solution;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;

class Zijihe {
    List<List<Integer>> result = new ArrayList<>(); // 存放符合条件的结果的集合
    LinkedList<Integer> path = new LinkedList<>(); // 用来存放符合条件的结果

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates); // 对数组进行排序
        dfs(candidates, target, 0);
        return result;
    }

    private void dfs(int[] candidates, int target, int startIndex) {
        if (target == 0) { // 找到符合条件的结果，将其加入到result中
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = startIndex; i < candidates.length; i++) {
            // 剪枝：如果当前元素已经大于target，那么后面的元素肯定也大于target，不需要再枚举
            if (candidates[i] > target) {
                break;
            }

            // 剪枝：如果当前元素与前一个元素相同，那么会出现重复解，直接跳过
            if (i > startIndex && candidates[i] == candidates[i - 1]) {
                continue;
            }

            path.add(candidates[i]); // 将当前元素加入到path中
            dfs(candidates, target - candidates[i], i + 1); // 递归处理剩余元素
            path.removeLast(); // 回溯，将当前元素从path中移除
        }
    }

    public static void main(String[] args) {
        int[] nums = {2,3,5,6,7};
        int target = 5;
        Zijihe solution = new Zijihe();
        List<List<Integer>> result = solution.combinationSum(nums, target);
        System.out.println(result);//[[2, 3], [5]]
    }
}

分支限界法

基本思想：在分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。

这个过程一直持续到找到所需的解或活结点表为空时为止。

搜索策略：在扩展结点处，先生成其所有的儿子结点（分支），然后再从当前的活结点表中选择下一个扩展结点。为了有效地选择下一扩展结点，加速搜索的进程，在每一个活结点处，计算一个函数值（限界），并根据函数值，从当前活结点表中选择一个最有利的结点作为扩展结点，使搜索朝着解空间上有最优解的分支推进，以便尽快地找出一个最优解。

经典例题：单源最短路径问题、装载问题、0-1背包问题

0-1背包问题

分支限界法求解0/1背包问题动画演示(Implementation of 0/1 Knapsack using Branch and Bound)_哔哩哔哩_bilibili

时间复杂度O(N*2^N)

例题

第一题

第二题贪心小数背包

假设有n个物品和一个背包，每个物品的重量为wi, 价值为pi，背包容量M。现在要将这n个物品（允许拆分,这里允许拆分说明这是小数背包问题）放入背包中，问怎样选择物品能使包中的物品总价值最大。

请给出用贪心算法解决此问题的贪心策略；

请给出用贪心算法解决此问题的基本步骤。

（1）最大性价比（单位重量的价值）优先策略。
（2）首先计算每种物品的性价比。然后，依贪心选择策略，将尽可能多的性价比最高的物品装入背包。若将这种物品全部装入背包后，背包内的物品总重量未超过C，则选择性价比次高的物品并尽可能多地装入背包。依此策略一直地进行下去，直到背包装满为止。

class Item {
    int weight; // 物品的重量
    int value;  // 物品的价值
    double unitValue; // 物品单位重量的价值

    public Item(int weight, int value) {
        this.weight = weight;
        this.value = value;
        this.unitValue = (double) value / weight; // 计算物品单位重量的价值
    }
}

class Solution {
    public double fractionalKnapsack(int[] weights, int[] values, int capacity) {
        List<Item> items = new ArrayList<>();
        for (int i = 0; i < weights.length; i++) {
            items.add(new Item(weights[i], values[i]));
        }

        // 按照物品单位重量的价值逆序排序
        items.sort((a, b) -> Double.compare(b.unitValue, a.unitValue));

        double maxValue = 0.0; // 最大价值
        for (Item item : items) {
            if (capacity <= 0) {
                break;
            }

            if (item.weight <= capacity) { // 物品可以完整装入背包中
                maxValue += item.value;
                capacity -= item.weight;
            } else { // 物品只能装入部分
                maxValue += capacity * item.unitValue;
                capacity = 0;
            }
        }

        return maxValue;
    }
}

其中，使用贪心算法来解决小数背包问题。首先将所有物品按照单位重量的价值逆序排序，然后对物品进行逐个选择，如果背包还有剩余容量，就将物品完整装入背包中，否则只能装入部分。最终返回所有物品的最大价值。

可以通过创建一个Solution对象并调用fractionalKnapsack方法来解决小数背包问题，例如：

int[] weights = {10, 20, 30};
int[] values = {60, 100, 120};
int capacity = 50;
Solution solution = new Solution();
double maxValue = solution.fractionalKnapsack(weights, values, capacity);
System.out.println(maxValue); // 输出最大价值

其中，weights为物品重量的数组，values为物品价值的数组，capacity为背包容量。可以通过输出maxValue来查看背包中物品的最大价值。

第三题 01背包动态规划

动态规划问题，这就是01背包问题的变种

第四题装载问题

现有3个货物要装上载重量为30的轮船，其中货物的重量分别为（16, 15, 15），要求在不超过轮船载重量的前提下，将尽可能多的货物（注意这里，是多装的货物重量，下面的bestw可以证明这个观点）装上轮船。
现使用回溯法要求：
（1）描述回溯法的基本思想；
（2）画出解空间树（包含所有可能解）；
（3）说明对问题的解空间树搜索时，采用什么策略避免无效搜索？
（4）回溯法搜索问题解空间树时，在解空间树上用×标注出在搜索过程中被剪枝的结点。

（1）回溯法的基本思想是在问题的解空间中，按照深度优先的策略，从根结点出发搜索整个解空间。在搜索过程中，如果发现某个结点不能满足问题的约束条件，或者已经搜索过，就回溯到上一个结点继续搜索。

（2）以下是问题的解空间树，其中每个结点表示一种可能的装载方案，左子树表示选择当前物品装载，右子树表示不选择当前物品装载。问题的最优解为装载数量最多的方案，因此需要优先搜索左子树。

（3）为了避免无效搜索，可以采用剪枝策略。在本问题中，由于要求尽可能多的装载货物，因此可以在搜索过程中，记录已经选中的货物重量之和，如果已经超过了轮船的载重量，就不再搜索当前结点的左子树，直接回溯到上一个结点继续搜索。

以下是一个使用回溯法解决该问题的Java代码实现：

import java.util.Arrays;

class Solution {
    int maxCount = 0;  // 最多可以装载的货物数量
    int[] weights;     // 货物重量
    boolean[] used;    // 记录货物是否被使用过

    public int loadShip(int[] weights, int capacity) {
        Arrays.sort(weights); // 对货物重量进行排序
        this.weights = weights;
        this.used = new boolean[weights.length];
        backtracking(0, 0, capacity);
        return maxCount;
    }

    private void backtracking(int index, int count, int capacity) {
        if (capacity == 0) { // 已经无法再装载货物了，记录当前已经装载的货物数量
            maxCount = Math.max(maxCount, count);
            return;
        }

        if (index == weights.length) { // 已经遍历完所有货物，返回
            return;
        }

        if (capacity >= weights[index]) { // 货物可以装载
            used[index] = true;
            backtracking(index + 1, count + 1, capacity - weights[index]); // 选择当前货物进行装载
            used[index] = false;
        }

        backtracking(index + 1, count, capacity); // 不选择当前货物进行装载
    }
}

其中，loadShip方法用于解决该问题，输入参数为货物重量的数组weights和轮船的载重量capacity，返回值为最多可以装载的货物数量。该方法首先对货物重量进行排序，然后调用backtracking方法进行回溯搜索。

backtracking方法用于搜索问题的解空间。输入参数index表示当前要考虑的货物的下标，count表示当前已经装载的货物数量，capacity表示当前轮船的剩余载重量。在搜索过程中，如果已经无法再装载更多的货物，就记录当前已经装载的货物数量，然后返回。如果已经遍历完所有的货物，则直接返回。如果当前货物可以装载，就选择当前货物进行装载，然后递归调用backtracking方法继续搜索。如果当前货物不能装载，就不选择当前货物进行装载，直接递归调用backtracking方法继续搜索。在方法的最后，需要将选择当前货物进行装载的状态恢复，以免影响后续搜索。

可以通过创建一个Solution对象并调用loadShip方法来解决该问题，例如：

int[] weights = {16, 15, 15};
int capacity = 30;
Solution solution = new Solution();
int maxCount = solution.loadShip(weights, capacity);
System.out.println(maxCount); // 输出最多可以装载的货物数量

其中，weights为货物重量的数组，capacity为轮船的载重量。可以通过输出maxCount来查看最多可以装载的货物数量。

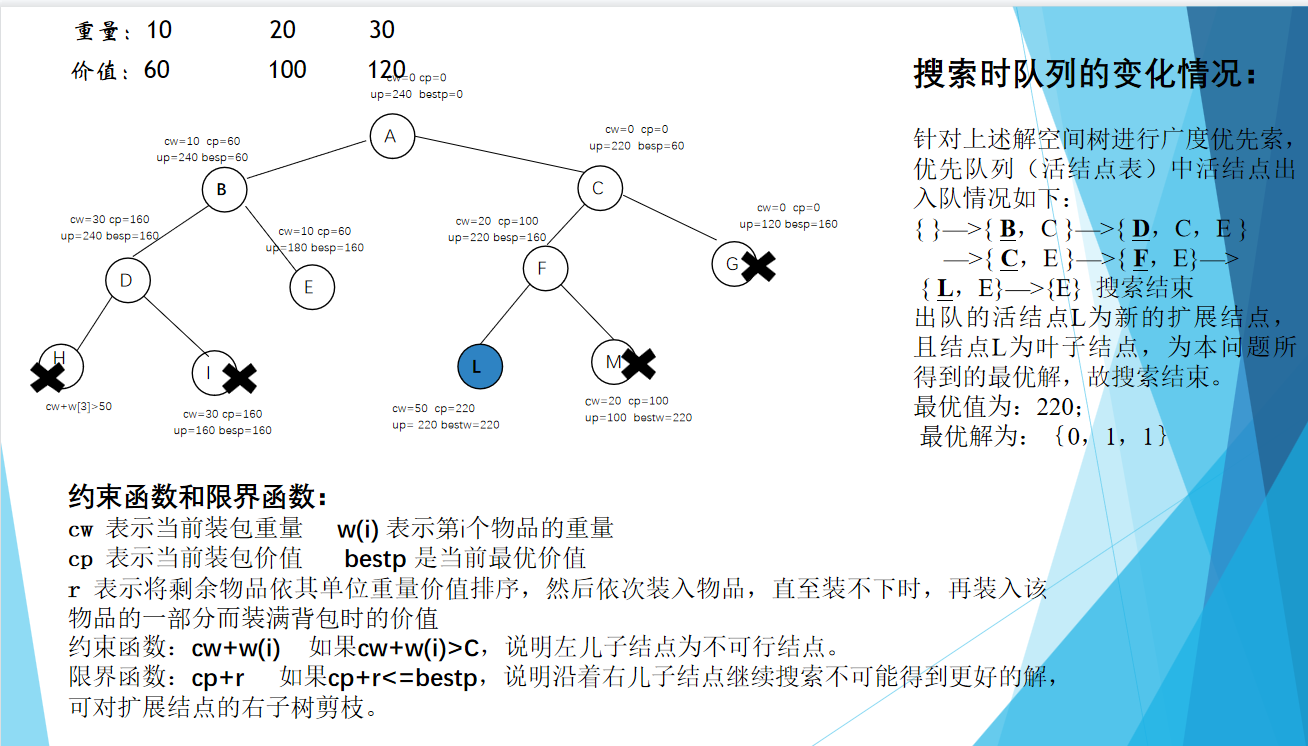
第五题分支界限法01背包问题

cp+rp>=bestp

rw>wk

活结点是经过约束函数和限界函数限制后存活下来的节点

扩展结点是活结点的两个子节点

分治法

归并排序

1. 基本思想

2. 实现逻辑

3. 动图演示

4. 复杂度分析

5. 代码实现

动态规划

0-1背包问题

贪心算法

最优装载问题

回溯法 （这个到时候看课本上的代码！！）

子集和问题

分支限界法

0-1背包问题

例题

第一题

第二题 贪心小数背包

第三题 01背包动态规划

第四题 装载问题

第五题 分支界限法01背包问题

回溯法（这个到时候看课本上的代码！！）

第二题贪心小数背包

第四题装载问题

第五题分支界限法01背包问题